Nptel Introduction To Machine Learning Assignment 2 Solution

 The parameters obtained in linear regression

 can take any value in the real space

 are strictly integers

 always lie in the range [0,1]

 can take only non-zero values

Suppose that we have N
 independent variables (X1,X2,...Xn
) and the dependent variable is Y
 . Now imagine that you are applying linear regression by fitting the best fit line using the least square error on this data. You found that the correlation coefficient for one of its variables (Say X1
) with Y
 is -0.005.

Regressing Y on X1 mostly does not explain away Y

 Regressing Y  on X1 explains away Y

 The given data is insufficient to determine if regressing Y on X1 explains away Y or not.

Which of the following is a limitation of subset selection methods in regression?

 They tend to produce biased estimates of the regression coefficients.

 They cannot handle datasets with missing values.

 They are computationally expensive for large datasets.

 They assume a linear relationship between the independent and dependent variables.

 They are not suitable for datasets with categorical predictors.

The relation between studying time (in hours) and grade on the final examination (0-100) in a random sample of students in the Introduction to Machine Learning Class was found to be:Grade = 30.5 + 15.2 (h)

How will a student’s grade be affected if she studies for four hours?

 It will go down by 30.4 points.

 It will go down by 30.4 points.

 It will go up by 60.8 points.

 The grade will remain unchanged.

 It cannot be determined from the information given

Which of the statements is/are True?

 Ridge has sparsity constraint, and it will drive coefficients with low values to 0.

 Lasso has a closed form solution for the optimization problem, but this is not the case for Ridge.

 Ridge regression does not reduce the number of variables since it never leads a coefficient to zero but only minimizes it.

 If there are two or more highly collinear variables, Lasso will select one of them randomly

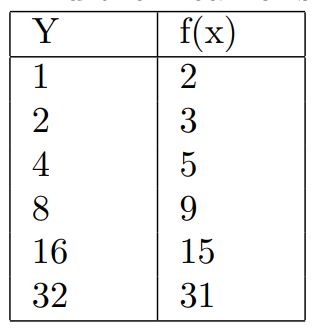
Find the mean of squared error for the given predictions:

Hint: Find the squared error for each prediction and take the mean of that.

 1

 2

 1.5

 0

Consider the following statements:
Statement A: In Forward stepwise selection, in each step, that variable is chosen which has the maximum correlation with the residual, then the residual is regressed on that variable, and it is added to the predictor.
Statement B: In Forward stagewise selection, the variables are added one by one to the previously selected variables to produce the best fit till then

 Both the statements are True.

 Statement A is True, and Statement B is False

 Statement A is False and Statement B is True

 Both the statements are False.

The linear regression model y=a0+a1x1+a2x2+...+apxp  is to be fitted to a set of N training data points having p attributes each. Let X be N×(p+1) vectors of input values (augmented by 1‘s), Y be N×1 vector of target values, and θ  be (p+1)×1 vector of parameter values (a0,a1,a2,...,ap). If the sum squared error is minimized for obtaining the optimal regression model, which of the following equation holds?

XTX=XY

Xθ=XTY

XTXθ=Y

XTXθ=XTY

Which of the following statements is true regarding Partial Least Squares (PLS) regression?

 PLS is a dimensionality reduction technique that maximizes the covariance between the predictors and the dependent variable.

 PLS is only applicable when there is no multicollinearity among the independent variables.

 PLS can handle situations where the number of predictors is larger than the number of observations.

 PLS estimates the regression coefficients by minimizing the residual sum of squares.

 PLS is based on the assumption of normally distributed residuals.

 All of the above.

 None of the above.

Which of the following statements about principal components in Principal Component Regression (PCR) is true?

 Principal components are calculated based on the correlation matrix of the original predictors.

 The first principal component explains the largest proportion of the variation in the dependent variable.

 Principal components are linear combinations of the original predictors that are uncorrelated with each other.

 PCR selects the principal components with the highest p-values for inclusion in the regression model.

 PCR always results in a lower model complexity compared to ordinary least squares regression.

Conclusion: #cryptograph, #nptel, #swayam, Data Analytics with Python, nptel, data science, data analytics, swyam, python for data science, Introduction To Machine Learning, Introduction to machine learning week 2 assignment solution, machine learning week 2 assignment solution, introduction to machine learning week 2 quiz answer, ML week 2 assignment answer